RESISTÊNCIA DOS MATERIAIS
Uma barra de latão de seção circular de diâmetro 3 cm está tracionada com uma força axial de 50 kN. Determinar a diminuição de seu diâmetro. São dados do material o módulo de elasticidade longitudinal de 1,08 . 104 kN/cm2 e o seu coeficiente de Poisson 0,3.
2,89.10-4 cm
5,89.10-4 cm
6,55.10-4 cm
1,96.10-4 cm
1,89.10-4 cm
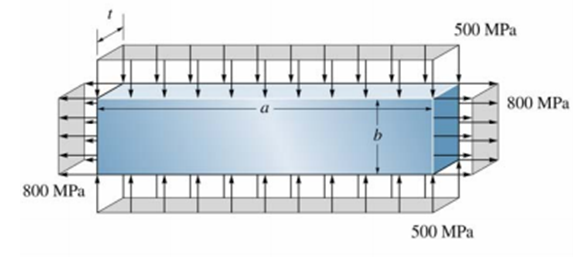
A barra de cobre da Figura está submetida a um carregamento uniforme ao longo de suas bordas como mostrado. Se ela tiver comprimento a=300 mm, largura b=50 mm e espessura t= 20 mm antes de a carga ser aplicada, determinar seus novos comprimento, largura e espessura após o carregamento. Adotar Ecu= 120 GPa, ν cu = 0,34.
a’ = 301,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 48,69 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 18,98 mm
a’ = 301,4 mm, b’ = 48,69 mm, t’ = 18,98 mm
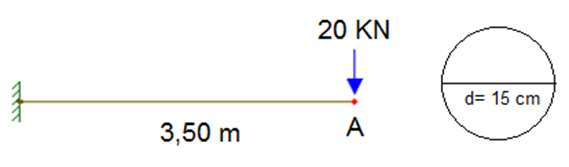
Determine para a viga abaixo, através do método de integrais sucessivas, a equação da linha elástica y(x) e da inclinação q(x). Com base nas equações obtidas assinale o valor correto do deslocamento no ponto A. Considere E = 200 GPa.
5,75 cm
3,25 cm
4,56 cm
2,22 cm
8,34 cm
O motor de engrenagens pode desenvolver 100 W quando gira a 80 rev/minuto. Se a tensão de cisalhamento admissível para o eixo for Tadm = 28 MPa, determine, com aproximação de múltiplos de 5 mm, o menor diâmetro do eixo que pode ser usado.

d = 25 mm
d = 35 mm
d = 10 mm
d = 20 mm
d = 15 mm
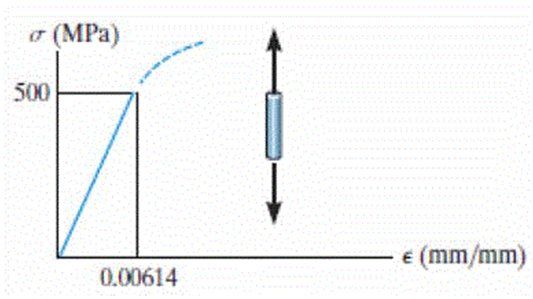
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50 mm e 12,5 mm de diâmetro. Quando a carga aplicada for 45 kN, o novo diâmetro do corpo de prova dará 12,48375 mm. Calcule o módulo de cisalhamento Gal = para o alumínio.
Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.

2,89.10-4 cm
5,89.10-4 cm
6,55.10-4 cm
1,96.10-4 cm
1,89.10-4 cm
A barra de cobre da Figura está submetida a um carregamento uniforme ao longo de suas bordas como mostrado. Se ela tiver comprimento a=300 mm, largura b=50 mm e espessura t= 20 mm antes de a carga ser aplicada, determinar seus novos comprimento, largura e espessura após o carregamento. Adotar Ecu= 120 GPa, ν cu = 0,34.

a’ = 301,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 48,69 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 18,98 mm
a’ = 301,4 mm, b’ = 48,69 mm, t’ = 18,98 mm
Determine para a viga abaixo, através do método de integrais sucessivas, a equação da linha elástica y(x) e da inclinação q(x). Com base nas equações obtidas assinale o valor correto do deslocamento no ponto A. Considere E = 200 GPa.

5,75 cm
3,25 cm
4,56 cm
2,22 cm
8,34 cm
O motor de engrenagens pode desenvolver 100 W quando gira a 80 rev/minuto. Se a tensão de cisalhamento admissível para o eixo for Tadm = 28 MPa, determine, com aproximação de múltiplos de 5 mm, o menor diâmetro do eixo que pode ser usado.

d = 25 mm
d = 35 mm
d = 10 mm
d = 20 mm
d = 15 mm
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50 mm e 12,5 mm de diâmetro. Quando a carga aplicada for 45 kN, o novo diâmetro do corpo de prova dará 12,48375 mm. Calcule o módulo de cisalhamento Gal = para o alumínio.

Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.


a’ = 301,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 48,69 mm, t’ = 19,98 mm
a’ = 302,4 mm, b’ = 49,68 mm, t’ = 18,98 mm
a’ = 301,4 mm, b’ = 48,69 mm, t’ = 18,98 mm
Determine para a viga abaixo, através do método de integrais sucessivas, a equação da linha elástica y(x) e da inclinação q(x). Com base nas equações obtidas assinale o valor correto do deslocamento no ponto A. Considere E = 200 GPa.

5,75 cm
3,25 cm
4,56 cm
2,22 cm
8,34 cm
O motor de engrenagens pode desenvolver 100 W quando gira a 80 rev/minuto. Se a tensão de cisalhamento admissível para o eixo for Tadm = 28 MPa, determine, com aproximação de múltiplos de 5 mm, o menor diâmetro do eixo que pode ser usado.

d = 25 mm
d = 35 mm
d = 10 mm
d = 20 mm
d = 15 mm
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50 mm e 12,5 mm de diâmetro. Quando a carga aplicada for 45 kN, o novo diâmetro do corpo de prova dará 12,48375 mm. Calcule o módulo de cisalhamento Gal = para o alumínio.

Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.


5,75 cm
3,25 cm
4,56 cm
2,22 cm
8,34 cm
O motor de engrenagens pode desenvolver 100 W quando gira a 80 rev/minuto. Se a tensão de cisalhamento admissível para o eixo for Tadm = 28 MPa, determine, com aproximação de múltiplos de 5 mm, o menor diâmetro do eixo que pode ser usado.

d = 25 mm
d = 35 mm
d = 10 mm
d = 20 mm
d = 15 mm
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50 mm e 12,5 mm de diâmetro. Quando a carga aplicada for 45 kN, o novo diâmetro do corpo de prova dará 12,48375 mm. Calcule o módulo de cisalhamento Gal = para o alumínio.

Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.

d = 25 mm
d = 35 mm
d = 10 mm
d = 20 mm
d = 15 mm
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50 mm e 12,5 mm de diâmetro. Quando a carga aplicada for 45 kN, o novo diâmetro do corpo de prova dará 12,48375 mm. Calcule o módulo de cisalhamento Gal = para o alumínio.

Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.


Gal = 36.10 GPa
Gal = 63.60 GPa
Gal = 33.50 GPa
Gal = 31.60 GPa
Gal = 13.60 GPa
A barra tem largura constante de 35 mm e espessura de 10 mm. Determine a tensão normal média máxima na barra quando ela é submetida à carga mostrada. Nota: a tensão normal média máxima será maior no local onde a carga máxima será maior, neste caso faça primeiramente o equilíbrio das forças.

